Equilíbrio de Hardy-Weinberg

A lei do equilíbrio de Hardy-Weinberg é uma importante forma de verificar se a seleção natural ou outros fatores evolutivos estão influenciando uma determinada população. Por meio da equação de Hardy-Weinberg, podemos determinar a configuração genética de uma população que não está sofrendo evolução. A partir dessa análise, podemos comparar os dados com as informações reais da população e, desse modo, perceber se há ou não evolução.

→ Hardy e Weinberg

Wilhelm Weinberg (1862-1937) e Godfrey Harold Hardy (1877-1947) foram os pesquisadores responsáveis pelas conclusões que levaram à criação da chamada lei do equilíbrio de Hardy-Weinberg.

Weinberg era um fisiologista alemão que se destacou por seus trabalhos com genética humana e genética médica, enquanto Hardy era um importante matemático inglês. Os dois pesquisadores chegaram às suas conclusões em 1908, de maneira independente e praticamente simultânea.

→ População em equilíbrio de Hardy-Weinberg

De acordo com Hardy e Weinberg, uma população que não está evoluindo apresenta, de uma geração para outra, frequência dos alelos e genótipos constante. Nesses casos, nos quais se observa apenas a recombinação de acordo com as leis de Mendel, dizemos que a população está em equilíbrio de Hardy-Weinberg.

→ Premissas para o estabelecimento do equilíbrio de Hardy-Weinberg

Uma população está em equilíbrio de Hardy-Weinberg quando suas frequências genotípicas e alélicas permanecem constantes. Para que o equilíbrio ocorra, a população analisada deverá obedecer algumas premissas. As condições essenciais para que uma população permaneça em equilíbrio de Hardy-Weinberg são:

• Ausência de seleção natural: para que uma população esteja em equilíbrio de Hardy-Weinberg, é necessário que a seleção natural não esteja atuando nela. Caso haja atuação da seleção natural, alguns genótipos serão selecionados, modificando as frequências alélicas da população.

• Ausência de mutações: mutações alteram o total de alelos presentes em uma população (pool gênico). Logo, em uma população em equilíbrio de Hardy-Weinberg, não ocorrem mutações.

• Ausência de fluxo gênico: quando há fluxo gênico, alguns genes podem ser incluídos ou excluídos da população. Desse modo, em uma situação de equilíbrio, não ocorre fluxo gênico.

• População grande: para que uma população esteja em equilíbrio, é importante que ela seja grande, pois populações pequenas favorecem a deriva genética (flutuações não previstas nas frequências alélicas de uma geração para outra).

• Mesmo número de machos e fêmeas na população.

• Todos os casais deverão ser férteis e gerar o mesmo número de filhotes.

• Cruzamentos ao acaso: para que ocorra o equilíbrio de Hardy-Weinberg, é necessário que os cruzamentos aconteçam de maneira aleatória, sem que ocorra preferência por determinados grupos dentro da população. Nesse caso, dizemos que a população está em panmixia, ou seja, todos acasalam-se de maneira aleatória.

→ Fórmula do equilíbrio de Hardy-Weinberg

A equação de Hardy-Weinberg deve ser usada para testar se uma população está ou não evoluindo. Considerando que existem dois alelos para um determinado locus, chamaremos o alelo dominante (p) de A, e o alelo recessivo (q) será chamado de a. Assim, p será a frequência alélica de A e q será a frequência de a, logo teremos que p + q = 1, uma vez que a soma desses dois alelos será igual a 100%.

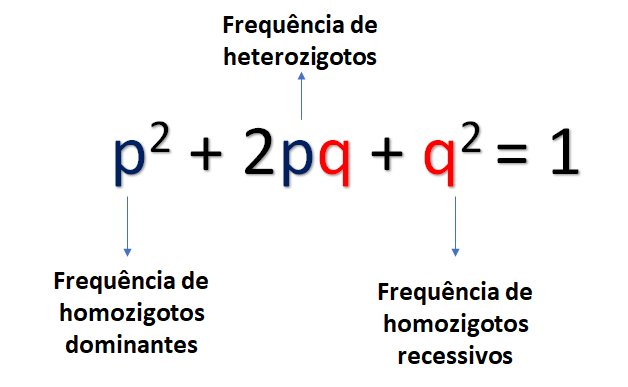
De acordo com o modelo de Hardy-Weiberg, teremos as frequências dos genótipos AA, Aa e aa representados, respectivamente, por p2, 2pq e q2. Isso se deve ao fato de que, para formar um indivíduo AA, é necessário um espermatozoide A e um óvulo A, cuja frequência é a mesma, portanto, p x p = p2. O mesmo raciocínio vale para o indivíduo aa. Já o heterezigoto (Aa) poderá resultar de um espermatozoide A e de um óvulo a, e vice-versa. A probabilidade de ocorrência é, portanto, 2 x p x q= 2pq. Desse modo, teremos:

Se somarmos todas as frequências, teremos 100%. Portanto, a fórmula do equilíbrio de Hardy-Weinberg é: