Exercícios Equilíbrio Hardy-Weinberg

Para exemplificar o que foi dito no post anterior, veja dois exercícios resolvidos a respeito do equilíbrio de Hardy-Weinberg:

1. (VUNESP) Em uma população em equilíbrio, constituída por 1000 indivíduos, 160 apresentam uma anomalia hereditária causada por um gene recessivo autossômico. Espera-se que sejam portadores desse gene recessivo, entre os indivíduos normais, o total de:

a) 480 indivíduos

b) 240 indivíduos

c) 160 indivíduos

d) 560 indivíduos

e) 840 indivíduos

Resolução

Se 160 indivíduos apresentam a anomalia, temos 16% dos indivíduos afetados:

q2 = 0,16

q = 0,4

Como p + q = 1, temos que:

p = 1 – q

p = 1 – 0,4

p = 0,6

O exercício pede que se encontre o número de indivíduos portadores do gene, ou seja, o número de indivíduos heterozigotos. Para calcular essa frequência, temos que:

F (Aa) = 2pq

F(Aa) = 2.0,6.0,4

F(Aa) = 0,48

Assim, a resposta é a alternativa a, pois 48% de 1000 indivíduos equivalem a 480 indivíduos.

2. (UFPI) Em 1908, os cientistas Hardy e Weinberg formularam um teorema cuja importância está no fato de estabelecer um modelo para o comportamento dos genes nas populações naturais. Se os valores das frequências gênicas de uma população, observada ao longo de gerações, forem significativamente diferentes dos valores esperados por meio da aplicação do teorema, pode-se concluir corretamente que:

a) A população estudada é infinitamente grande, inviabilizando a aplicação do teorema.

b) Não houve a atuação dos fatores evolutivos sobre a população.

c) A população encontra-se em equilíbrio genético.

d) A população está evoluindo, uma vez que as frequências gênicas foram alteradas.

e) Os cruzamentos nessa população ocorrem ao acaso.


Resolução

O exercício pede uma definição bastante simples relacionada ao equilíbrio de Hardy-Weinberg. Considerando que uma população em equilíbrio não está sofrendo a ação de fatores evolutivos, podemos concluir que, se os valores das frequências forem diferentes dos valores esperados, a população está evoluindo. A resposta, portanto, é a alternativa d.

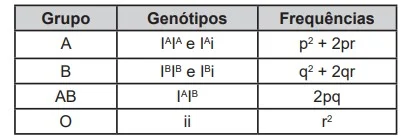
3. (ENEM) Uma população encontra-se em equilíbrio genético quanto ao sistema ABO, em que 25% dos indivíduos pertencem ao grupo O e 16%, ao grupo A homozigotos. Considerando que: p = frequência de IA; q = frequência de IB; e r = frequência de i, espera-se encontrar:

A porcentagem de doadores compatíveis para alguém do grupo B nessa população deve ser de:

a) 11%.

b) 19%.

c) 26%.

d) 36%.

e) 60%